Ames Housing

Project: Linear Regression With Housing Data

Allen Jackson

In the following code cells I create three functions in order to run variable linear regressions on the Ames Housing dataset. The dataset contains over 80 variables with information on sold houses. I first can transform the data, dropping columns and filling in missing values. I then can select columns based on a correlation threshold. Finally, I can train and test the final dataset using my choice of k folds.

import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import KFold
pd.set_option("display.max_columns", 999)
pd.set_option("display.max_rows", 1000)

Housing = pd.read_csv('AmesHousing.tsv', delimiter = '\t')
Housing1 = Housing

Many of the columns in this dataframe contain a large amount of missing values. The following code filters columns with a certain amount of missing values (the default value is 25%) and imputes the rest with the most common value in its respective column.

def transform_features(Dataframe, NA_limit = .25):
    # Drop Empty columns based on amount of missing data
    Percent_null = Housing1.isnull().sum()/len(Dataframe)
    Dataframe = Dataframe.drop(Percent_null[Percent_null > NA_limit].index, axis = 1)

    # Drop Categoricals with missing values
    Categoricals = Dataframe.select_dtypes(include=['object']).isnull().sum()
    Dropped_Categoricals = Categoricals[Categoricals > 0]
    Dataframe = Dataframe.drop(Dropped_Categoricals.index, axis = 1)

    #Impute Numerical Values with mode
    Dataframe_numerical = Dataframe.select_dtypes(include=['int', 'float'])    
    for feature in Dataframe_numerical.columns:
        Dataframe[feature].fillna(Dataframe[feature].mode()[0], inplace = True)
    # Build New Variables
    years_since_remod = Dataframe['Yr Sold'] - Dataframe['Year Remod/Add']
    Dataframe['years_since_remod'] = years_since_remod

    # Drop Useless Variables
    Dataframe = Dataframe.drop(['Sale Type','Sale Condition', 'Order', 'PID',
                    'Mo Sold', 'Misc Val', 'Year Built', 'Year Remod/Add', 'Yr Sold'], axis = 1)
    return Dataframe
House_Transformed = transform_features(Housing1)

Correlation_Index = abs(House_Transformed.corr()['SalePrice']).sort_values().index
fig = plt.figure(figsize=(10, 20)) # the 10 here is width, the 3 is height
ax = fig.add_subplot()
ax.barh(Correlation_Index,abs(House_Transformed.corr()['SalePrice']).sort_values())

plt.show(fig)

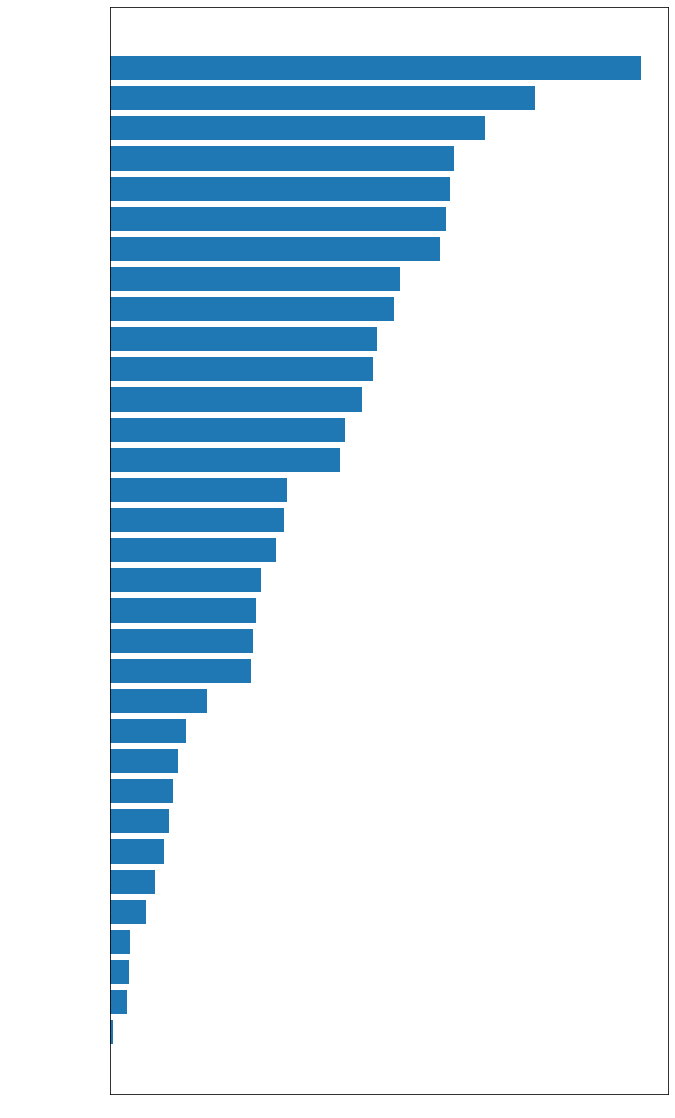
The graph above shows the correlations level between said column and Sale Price. Columns with low correlation won’t add information to this regression. Thus the following code sets an acceptable level of correlation and then deletes columns which don’t reach that level. The code also filters columns that don’t have any variation as these columns won’t increase the models ability to predict values. Finally, all the remaining categorical variables are transformed into dummies.

def select_features(Dataframe, Correlation_cutoff = .3, Value_threshold = 4):
    #Drop columns on correlation criteria
    correlations = abs(Dataframe.corr()['SalePrice']).sort_values()
    Dataframe = Dataframe.drop(correlations[correlations < Correlation_cutoff].index, axis = 1)

    # Filter non unique categorical columns
    Dataframe_categorical = Dataframe.select_dtypes(include=['object'])
    number_unique_values = {}
    for feature in Dataframe_categorical.columns:
        number_unique_values[feature] = len(Dataframe_categorical[feature].value_counts())
    for key in number_unique_values:
        if number_unique_values[key] <= Value_threshold:
            Dataframe.drop(key, axis = 1)
    # Transform object types to category types
    for feature in Dataframe_categorical.columns:
        Dataframe[feature] = Dataframe[feature].astype('category')

    #Transform into dummy variables and remove old features
    Dataframe = pd.concat([Dataframe,
            pd.get_dummies(Dataframe.select_dtypes(include=['category']))
            ], axis=1).drop(Dataframe_categorical.columns, axis=1)

    return Dataframe
House_Select = select_features(House_Transformed)
House_Select

	Lot Frontage	Overall Qual	Mas Vnr Area	BsmtFin SF 1	Total Bsmt SF	1st Flr SF	Gr Liv Area	Full Bath	TotRms AbvGrd	Fireplaces	Garage Yr Blt	Garage Cars	Garage Area	Wood Deck SF	Open Porch SF	SalePrice	years_since_remod	MS Zoning_A (agr)	MS Zoning_C (all)	MS Zoning_FV	MS Zoning_I (all)	MS Zoning_RH	MS Zoning_RL	MS Zoning_RM	Street_Grvl	Street_Pave	Lot Shape_IR1	Lot Shape_IR2	Lot Shape_IR3	Lot Shape_Reg	Land Contour_Bnk	Land Contour_HLS	Land Contour_Low	Land Contour_Lvl	Utilities_AllPub	Utilities_NoSeWa	Utilities_NoSewr	Lot Config_Corner	Lot Config_CulDSac	Lot Config_FR2	Lot Config_FR3	Lot Config_Inside	Land Slope_Gtl	Land Slope_Mod	Land Slope_Sev	Neighborhood_Blmngtn	Neighborhood_Blueste	Neighborhood_BrDale	Neighborhood_BrkSide	Neighborhood_ClearCr	Neighborhood_CollgCr	Neighborhood_Crawfor	Neighborhood_Edwards	Neighborhood_Gilbert	Neighborhood_Greens	Neighborhood_GrnHill	Neighborhood_IDOTRR	Neighborhood_Landmrk	Neighborhood_MeadowV	Neighborhood_Mitchel	Neighborhood_NAmes	Neighborhood_NPkVill	Neighborhood_NWAmes	Neighborhood_NoRidge	Neighborhood_NridgHt	Neighborhood_OldTown	Neighborhood_SWISU	Neighborhood_Sawyer	Neighborhood_SawyerW	Neighborhood_Somerst	Neighborhood_StoneBr	Neighborhood_Timber	Neighborhood_Veenker	Condition 1_Artery	Condition 1_Feedr	Condition 1_Norm	Condition 1_PosA	Condition 1_PosN	Condition 1_RRAe	Condition 1_RRAn	Condition 1_RRNe	Condition 1_RRNn	Condition 2_Artery	Condition 2_Feedr	Condition 2_Norm	Condition 2_PosA	Condition 2_PosN	Condition 2_RRAe	Condition 2_RRAn	Condition 2_RRNn	Bldg Type_1Fam	Bldg Type_2fmCon	Bldg Type_Duplex	Bldg Type_Twnhs	Bldg Type_TwnhsE	House Style_1.5Fin	House Style_1.5Unf	House Style_1Story	House Style_2.5Fin	House Style_2.5Unf	House Style_2Story	House Style_SFoyer	House Style_SLvl	Roof Style_Flat	Roof Style_Gable	Roof Style_Gambrel	Roof Style_Hip	Roof Style_Mansard	Roof Style_Shed	Roof Matl_ClyTile	Roof Matl_CompShg	Roof Matl_Membran	Roof Matl_Metal	Roof Matl_Roll	Roof Matl_Tar&Grv	Roof Matl_WdShake	Roof Matl_WdShngl	Exterior 1st_AsbShng	Exterior 1st_AsphShn	Exterior 1st_BrkComm	Exterior 1st_BrkFace	Exterior 1st_CBlock	Exterior 1st_CemntBd	Exterior 1st_HdBoard	Exterior 1st_ImStucc	Exterior 1st_MetalSd	Exterior 1st_Plywood	Exterior 1st_PreCast	Exterior 1st_Stone	Exterior 1st_Stucco	Exterior 1st_VinylSd	Exterior 1st_Wd Sdng	Exterior 1st_WdShing	Exterior 2nd_AsbShng	Exterior 2nd_AsphShn	Exterior 2nd_Brk Cmn	Exterior 2nd_BrkFace	Exterior 2nd_CBlock	Exterior 2nd_CmentBd	Exterior 2nd_HdBoard	Exterior 2nd_ImStucc	Exterior 2nd_MetalSd	Exterior 2nd_Other	Exterior 2nd_Plywood	Exterior 2nd_PreCast	Exterior 2nd_Stone	Exterior 2nd_Stucco	Exterior 2nd_VinylSd	Exterior 2nd_Wd Sdng	Exterior 2nd_Wd Shng	Exter Qual_Ex	Exter Qual_Fa	Exter Qual_Gd	Exter Qual_TA	Exter Cond_Ex	Exter Cond_Fa	Exter Cond_Gd	Exter Cond_Po	Exter Cond_TA	Foundation_BrkTil	Foundation_CBlock	Foundation_PConc	Foundation_Slab	Foundation_Stone	Foundation_Wood	Heating_Floor	Heating_GasA	Heating_GasW	Heating_Grav	Heating_OthW	Heating_Wall	Heating QC_Ex	Heating QC_Fa	Heating QC_Gd	Heating QC_Po	Heating QC_TA	Central Air_N	Central Air_Y	Kitchen Qual_Ex	Kitchen Qual_Fa	Kitchen Qual_Gd	Kitchen Qual_Po	Kitchen Qual_TA	Functional_Maj1	Functional_Maj2	Functional_Min1	Functional_Min2	Functional_Mod	Functional_Sal	Functional_Sev	Functional_Typ	Paved Drive_N	Paved Drive_P	Paved Drive_Y
0	141.0	6	112.0	639.0	1080.0	1656	1656	1	7	2	1960.0	2.0	528.0	210	62	215000	50	0	0	0	0	0	1	0	0	1	1	0	0	0	0	0	0	1	1	0	0	1	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	1	0	0	0	0	0	1	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	1	0	0	0	1	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	1	0	0	0	0	1	0	1	0	0	0	0	0	1	0	0	0	0	0	1	0	0	0	0	1	0	0	0	0	1	0	0	0	0	0	0	0	1	0	1	0
1	80.0	5	0.0	468.0	882.0	896	896	1	5	0	1961.0	1.0	730.0	140	0	105000	49	0	0	0	0	1	0	0	0	1	0	0	0	1	0	0	0	1	1	0	0	0	0	0	0	1	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	1	0	0	0	0	0	0	1	0	0	0	0	0	0	1	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	1	0	0	0	0	1	0	1	0	0	0	0	0	1	0	0	0	0	0	0	0	0	1	0	1	0	0	0	0	1	0	0	0	0	0	0	0	1	0	0	1
2	81.0	6	108.0	923.0	1329.0	1329	1329	1	6	0	1958.0	1.0	312.0	393	36	172000	52	0	0	0	0	0	1	0	0	1	1	0	0	0	0	0	0	1	1	0	0	1	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	1	0	0	0	0	0	1	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	1	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	1	0	0	0	0	1	0	1	0	0	0	0	0	1	0	0	0	0	0	0	0	0	1	0	1	0	0	1	0	0	0	0	0	0	0	0	0	1	0	0	1
3	93.0	7	0.0	1065.0	2110.0	2110	2110	2	8	2	1968.0	2.0	522.0	0	0	244000	42	0	0	0	0	0	1	0	0	1	0	0	0	1	0	0	0	1	1	0	0	1	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	1	0	0	0	0	0	1	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	1	0	0	0	1	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	1	0	1	0	0	0	0	0	1	0	0	0	0	1	0	0	0	0	0	1	1	0	0	0	0	0	0	0	0	0	0	0	1	0	0	1
4	74.0	5	0.0	791.0	928.0	928	1629	2	6	1	1997.0	2.0	482.0	212	34	189900	12	0	0	0	0	0	1	0	0	1	1	0	0	0	0	0	0	1	1	0	0	0	0	0	0	1	1	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	1	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	1	0	0	0	1	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	1	0	0	0	0	1	0	0	1	0	0	0	0	1	0	0	0	0	0	0	1	0	0	0	1	0	0	0	0	1	0	0	0	0	0	0	0	1	0	0	1
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
2925	37.0	6	0.0	819.0	1003.0	1003	1003	1	6	0	1984.0	2.0	588.0	120	0	142500	22	0	0	0	0	0	1	0	0	1	1	0	0	0	0	0	0	1	1	0	0	0	1	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	1	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	1	0	1	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	1	0	1	0	0	0	0	0	1	0	0	0	0	0	0	0	0	1	0	1	0	0	0	0	1	0	0	0	0	0	0	0	1	0	0	1
2926	60.0	5	0.0	301.0	864.0	902	902	1	5	0	1983.0	2.0	484.0	164	0	131000	23	0	0	0	0	0	1	0	0	1	1	0	0	0	0	0	1	0	1	0	0	0	0	0	0	1	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	1	0	0	0	0	0	1	0	0	0	0	0	0	1	0	0	0	0	0	0	1	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	1	0	1	0	0	0	0	0	1	0	0	0	0	0	0	0	0	1	0	1	0	0	0	0	1	0	0	0	0	0	0	0	1	0	0	1
2927	62.0	5	0.0	337.0	912.0	970	970	1	6	0	2005.0	0.0	0.0	80	32	132000	14	0	0	0	0	0	1	0	0	1	0	0	0	1	0	0	0	1	1	0	0	0	0	0	0	1	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	1	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	1	0	0	1	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	1	0	0	0	0	1	0	0	1	0	0	0	0	1	0	0	0	0	0	0	0	0	1	0	1	0	0	0	0	1	0	0	0	0	0	0	0	1	0	0	1
2928	77.0	5	0.0	1071.0	1389.0	1389	1389	1	6	1	1975.0	2.0	418.0	240	38	170000	31	0	0	0	0	0	1	0	0	1	0	0	0	1	0	0	0	1	1	0	0	0	0	0	0	1	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	1	0	0	0	0	0	1	0	0	0	0	0	0	1	0	0	0	0	0	0	1	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	1	0	1	0	0	0	0	0	1	0	0	0	0	0	0	1	0	0	0	1	0	0	0	0	1	0	0	0	0	0	0	0	1	0	0	1
2929	74.0	7	94.0	758.0	996.0	996	2000	2	9	1	1993.0	3.0	650.0	190	48	188000	12	0	0	0	0	0	1	0	0	1	0	0	0	1	0	0	0	1	1	0	0	0	0	0	0	1	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	1	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	1	0	0	0	1	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	1	0	0	1	0	0	0	0	1	0	0	0	0	1	0	0	0	0	0	1	0	0	0	0	1	0	0	0	0	0	0	0	1	0	0	1

2930 rows × 194 columns

The following code runs a linear regression. Changing the value of the parameter k will change whether or not the rows or randomized as well as what folding technique is used to test the data.The final test uses a test with two folds in and results in a root mean squared error of 36450. Any of the previously mentioned parameters can be changed in order to create an optimal Linear Regression.

def train_and_test(Dataframe, k = 0):
    features = Dataframe.select_dtypes(include=['int64', 'float']).columns.drop('SalePrice')
    if k == 0:
        Division = int(len(Dataframe)/Divider)
        train = Dataframe[:Division]
        test = Dataframe[Division:]
        mlr = LinearRegression()
        mlr.fit(train[features], train['SalePrice'])
        prediction = mlr.predict(test[features])
        rmse = mean_squared_error(test['SalePrice'], prediction) ** 1/2
        return rmse
    if k == 1:
        Division = int(len(Dataframe)/Divider)
        Dataframe = Dataframe.sample(frac = 1)
        train = Dataframe[:Division]
        test = Dataframe[Division:]

        mlr1 = LinearRegression()
        mlr1.fit(train[features], train['SalePrice'])
        prediction1 = mlr1.predict(test[features])
        rmse1 = mean_squared_error(test['SalePrice'], prediction1) ** 1/2

        mlr2 = LinearRegression()
        mlr2.fit(test[features], test['SalePrice'])
        prediction2 = mlr2.predict(train[features])
        rmse2 = mean_squared_error(train['SalePrice'], prediction2) ** 1/2

        avg_rmse = (rmse1 + rmse2)/2

        return avg_rmse

    else:
        kf = KFold(n_splits=k, shuffle=True)
        rmse_values = []
        for train_index, test_index, in kf.split(Dataframe):
            train = Dataframe.iloc[train_index]
            test = Dataframe.iloc[test_index]
            mlr = LinearRegression()
            mlr.fit(train[features], train["SalePrice"])
            predictions = mlr.predict(test[features])
            mse = mean_squared_error(test["SalePrice"], predictions)
            rmse = np.sqrt(mse)
            rmse_values.append(rmse)
        print(rmse_values)
        avg_rmse = np.mean(rmse_values)
        return avg_rmse
train_and_test(House_Select, k = 2)

[33369.68782332669, 39531.090901945376]





36450.38936263604